10050. Самый
длинный путь в дереве
Задано
неориентированное взвешенное дерево. Найдите в нем самый длинный путь. То есть
найдите такие две вершины, расстояние между которыми максимально.
Вход. Первая строка содержит
количество вершин в дереве n (2
≤ n ≤ 105).
Следующие n – 1 строка
описывают ребра. Каждая строка содержит три целых числа: номера вершин,
соединенных ребром (вершины пронумерованы числами от 1 до n), и вес ребра w (1
≤ w ≤ 105).
Выход. Выведите длину самого длинного
пути в дереве.
|
Пример
входа |
Пример
выхода |
|
6 1 2 3 2 3 4 2 6 2 6 4 6 6 5 5 |
12 |
РЕШЕНИЕ
поиск в
ширину
Анализ алгоритма
Кратчайший путь во взвешенном дереве можно
найти с помощью поиска в глубину или ширину (использование алгоритма Дейкстры в
данном случае не обязательно).
Для нахождения
самого длинного пути (диаметра дерева) действуем следующим образом:
1.
Выполним поиск в ширину из первой вершины. Найдем вершину v,
до которой путь будет наибольшим.
2.
Затем запустим поиск в ширину из вершины v и
определим вершину u, до которой путь также будет наибольшим.
3.
Путь от v до u является самым длинным в
дереве (диаметром дерева).
Пример
Дерево, представленное в
примере, имеет следующий вид:
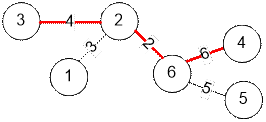
·
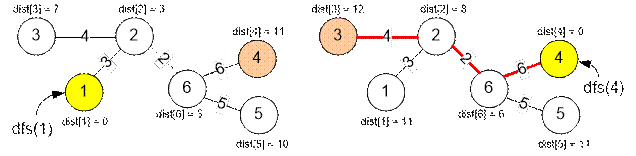
Выполним поиск в ширину из вершины 1 (слева). Самый
длинный путь будет до вершины 4.
·
Затем запустим поиск в ширину из вершины 4 (справа). Самый
длинный путь окажется до вершины 3, его длина равна 12.
Реализация алгоритма
Объявим список смежности графа g.
Объявим массив
кратчайших расстояний d.
vector<vector<pair<int, int>> > g;
vector<long long> d;
Функция bfs выполняет поиск в ширину
из вершины v.
int bfs(int v)
{
deque<int> q;
q.push_back(v);
while (!q.empty())
{
int v = q.front(); q.pop_front();
for (auto x : g[v])
{
int to = x.first;
int w = x.second;
if (d[to] == -1)
{
d[to] = d[v] + w;
q.push_back(to);
}
}
}
Возвращаем номер
вершины, до которой расстояние от
вершины v максимально.
return max_element(d.begin() + 1, d.begin() + n + 1) - d.begin();
}
Основная часть
программы. Читаем входные данные. Строим граф.
scanf("%d", &n);
g.resize(n + 1);
for (i = 0; i < n - 1; i++)
{
scanf("%d %d
%lld", &b, &e, &dist);
g[b].push_back({ e, dist });
g[e].push_back({ b, dist });
}
Инициализируем массив
кратчайших расстояний.
d = vector<long long>(n + 1, -1);
d[1] = 0;
Выполняем первый поиск в ширину из вершины 1. Определяем вершину v, которая находится дальше
всего от 1.
int v = bfs(1);
Снова инициализируем массив кратчайших расстояний и запускаем второй
поиск в ширину, начиная с вершины v.
d = vector<long long>(n + 1, -1);
d[v] = 0;
v = bfs(v);
Выводим ответ –
длину наибольшего пути.
printf("%lld\n", d[v]);
Реализация алгоритма – поиск в глубину
Список смежности
графа храним в массиве g.
Для хранения кратчайших
расстояний объявим массив dist.
vector<vector<pair<int, int>> > g;
vector<long long> dist;
Функция dfs выполняет поиск в глубину
из вершины v. Вершина p является предком
v в
процессе поиска в глубину.
void dfs(int v, int p = -1)
{
Перебираем все ребра,
смежные с вершиной v.
for (auto x : g[v])
{
Рассматриваем ребро v → to с весом w.
int to = x.first;
int w = x.second;
Если to ≠ p, пересчитываем dist[to]
и вызываем поиск в глубину из вершины to.
if (to != p)
{
dist[to] = dist[v] + w;
dfs(to, v);
}
}
}
Основная часть
программы. Читаем входные данные. Строим граф.
scanf("%d", &n);
g.resize(n + 1);
for (i = 0; i < n - 1; i++)
{
scanf("%d %d
%d", &b, &e, &w);
g[b].push_back({ e,
w });
g[e].push_back({ b,
w });
}
Выполняем поиск в глубину из вершины 1. Заполняем массив кратчайших
расстояний dist от вершины 1.
dist.assign(n + 1, -1);
dist[1] = 0;
dfs(1);
Определяем вершину v, расстояние до которой от вершины 1 максимально.
v = max_element(dist.begin(),
dist.end()) - dist.begin();
Выполняем второй поиск в
глубину, начиная с вершины v. Заполняем массив кратчайших расстояний dist
от вершины v.
dist.assign(n + 1, -1);
dist[v] = 0;
dfs(v);
Наибольшее
значение в массиве dist равно диаметру дерева.
v = max_element(dist.begin(), dist.end()) - dist.begin();
Выводим ответ.
printf("%lld\n", dist[v]);
Python реализация
from collections import deque
Читаем входные
данные. Список смежности графа храним в g.
Объявляем список
кратчайших расстояний d.
n = int(input())
g = [[] for _ in range(n + 1)]
d = [-1] * (n + 1)
Строим граф.
for _ in
range(n - 1):
b, e, dist = map(int, input().split())
g[b].append((e,
dist))
g[e].append((b,
dist))
Функция bfs выполняет поиск в ширину
из вершины v.
def bfs(v):
q = deque()
q.append(v)
while
q:
v = q.popleft()
for
to, w in g[v]:
if
d[to] == -1:
d[to] = d[v]
+ w
q.append(to)
Возвращаем номер
вершины, до которой расстояние от
вершины v максимально.
return
d.index(max(d))
Выполняем первый поиск в ширину из вершины 1. Определяем вершину v, которая находится дальше
всего от 1.
d[1] = 0
v = bfs(1)
Инициализируем
массив кратчайших расстояний и запускаем второй
поиск в ширину из вершины v.
d = [-1] * (n + 1)
d[v] = 0
v = bfs(v)
Выводим ответ –
длину наибольшего пути.
print(d[v])